LABYRENTH CTF WINDOWS TRACK CHALLENGE #9

File: DelphiChallenge.exe

SHA256: A2A27852B07B10CC02C9767A4AF2D9905C1CAB131E9411DDD9BC04FA67D4E62F

Packed: Yes

Architecture: 32Bit

Tools used: exeinfo, IDA Pro, OllyDbg

Codes & Binaries: https://github.com/jmprsp/labyrenth/tree/master/Window-Challenge-9

Description: This challenge is written in Delphi. Unpack it and reverse to get the flag.

Figure 1. Evidence of the challenge being packed

Needless to say much. The challenge is packed. Let’s Unpack it shall we =)

Looking at IDA Pro we can see the following jmp instruction at the end of the graph. Tracing the jmp instructions bring us to the figure below. @0x6F10CA the codes doesn’t look right… Perhaps we could place a breakpoint @0x6F1865 and look into it.

Figure 2. IDA Pro suspicious jump

On hitting the breakpoint @0x6F1865 , we can see that 0x6F10CA had been modified.

Figure 3. In memory code modification

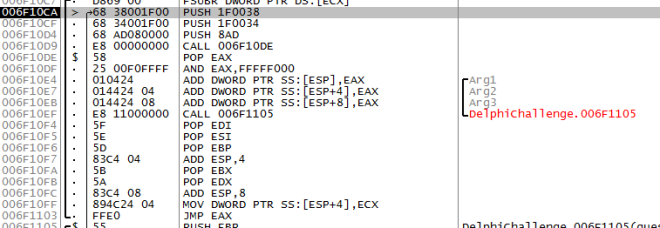
Now let’s take a look at the memory map (figure 4). So far there are nothing of interest here…

Figure 4. Memory Map

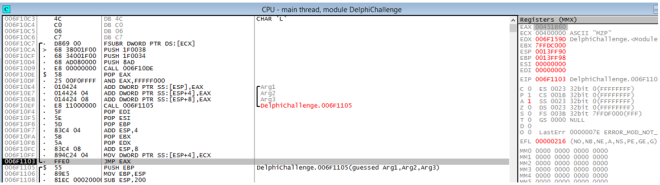
Interestingly after calling the function @0x006f1105, the memory maps get filled with tons of stuff. A interesting thing to note is the EAX (OEP) after calling 0x006f1105. Seems to me that the original code has been unpack to 0x400000 memory range….

Figure 5. Code unpacked

To prove that 0x400000 contains the original code and not some random heap allocation… Let’s take a look at its content. From the figure below, we can clearly see that an executable has been copied to the memory @0x400000.

Figure 6. MZ Header spotted

In the following figure we can see a jmp to EAX; the OEP of the original challenge.

Figure 7. jmp EAX

Take the jmp and dump the process using the ollydbg plugin as shown below.

Figure 8. dumping process

However, the dumped process fails to run properly… looks like we need to fix the import table.Fire up Scylla tool and fix the dump!

Figure 9. Fixing the dump

Note that while Scylla managed to locate the VA, it fails to detect the correct size initially. We could use ollydbg to identify the size and enter it manually into Scylla as shown above.

Figure 10. End of imports

You may find the unpack challenge at the github link provided. On execution, you should see the following user interface.

Figure 11. Delphi Challenge unpacked

Back to finding flag!

Let’s do a search for the text “wrong” in IDA Pro.

Figure 12. _TFORM1_Timer1Timer?

Let’s do some x-referencing…

Figure 13. x-referencing

Figure 14. Label3Click

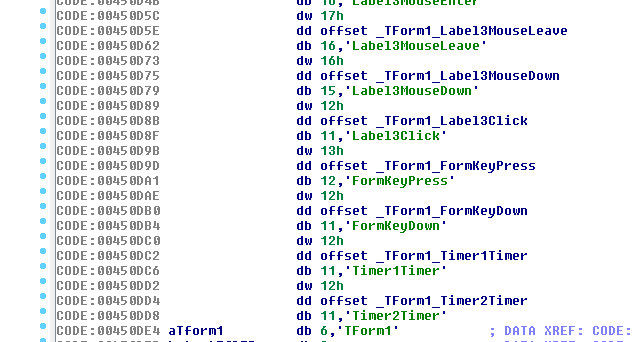
Tracing from click we arrive at the following function… in which we can observe something of interest. A comparison of “PAN{“. So we know that the flag is near… once we click on Enter button, this function gets triggered and there is a check on the key entered.

Figure 15. PAN{

further down we see how the 5th character of the flag is encoded. @0x00450F3D we can see that it is trying to cmp ebx with 0xCF. This value is derived after xoring with 0xAB @0x00450F37. Doing the math… 0xCF ^ 0xAB == 0x64 (ASCII D) therefore the 5th character is D.

Figure 16. FLAG_5

Instead of having multiple screenshots here… i shall cut it short using a table. To see how the flag is derived, trace upwards from the cmp address provided. Note that when we try to reverse a shift right operation, we would lose some data… therefore there are some cases where we need to guess what is the exact value. e.g. pos 14.

pos	cmp address	Math Transformation	Value
1	0x00450EAF	None	P
2	0x00450ECD	None	A
3	0x00450EEB	None	N
4	0x00450F09	None	{
5	0x00450F3D	0xCF ^ 0xAB = 0x64	d
6	0x00450F4C	0x1E ^ 0x2D = 0x33	3
7	0x00450FA0	0x52 ^ 0x3E = 0x6C	l
8	0x00450FAC	0x52 ^ 0x22 = 0x70	p
9	0x00450FBB	0x60 & 0x8 =  0x68	h
10	0x00450FC5	0x68 + 1 = 0x69	i
11	0x00450FE6	0xBA ^ 0xE5 = 0x5F	_
12	0x0045100A	0xBE ^ 0xD7 = 0x69	i
13	0x00451060	0xE6 / 2 = 0x73	s
14	0x0045106E	0x2F << 1 = 0x5E	_ or ^
15	0x0045107D	0x194 >> 2 = 0x65	e
16	0x0045108E	(0x19 << 1) + 2 = 0x34	4
17	0x004510E5	(0x1C0 ^ 0xC) >> 2 = 0x73	s
18	0x004510F6	(0x38 & 0x4) << 1 = 0x78	x or y
19	0x00451107	(0x28 + 0x7) << 1 = 0x5E	_ or ^
20	0x00451118	((0x8C / 5) / 2) << 3 = 0x70	p – w
21	0x00451137	0x60 / 2 = 0x30	0
22	0x00451155	0x17c >> 2 = 0x5F	_
23	0x00451178	(0x59 ^ 0x60) << 1 = 0x72	r or t
24	0x0045119B	(0x42 ^ 0x88) / 2 = 0x65	e
25	0x004511BD	(0x2C ^ 0xC0) / 2 = 0x76	v
26	0x004511DF	(0x16 << 1) + 7 = 0x33	3
27	0x00451206	(0x36 ^ 0x29A) / 3/ 2 = 0x72	r
28	0x0045122A	(0x130F0 >> 3) ^ 0x2486 >> 3 == 0x53	S
29	0x0045124E	((0x2950 ^ 0x25A0) >> 4) / 3 = 0x45	E

Figure 17. Flag secured!

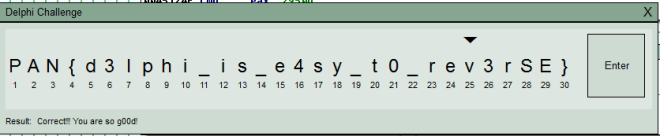
FLAG: PAN{d3lphi_is_e4sy_t0_rev3rSE}